Season's greetings.
For your Christmas reading, this blog usually provides a seasonally appropriate post on fast food, including to date posts about: nutrition (McDonald's fast-food), geography (Fast-food maps) and diet (Fast food and diet). This year, we will update some of the geographical and diet information about the effects of fast food on people worldwide.
First, there seems to be a general perception that access to fast food is continuing to increase in the modern world, even though that increase started more than half a century ago. Such a perception is easy to verify in the USA, as shown in a previous post (Fast-food maps). However, this trend also appears globally.
For example, in 2013 the Guardian newspaper produced a dataset (called the McMap of the World) illustrating the recent growth in the number of McDonald's restaurants worldwide (McDonald's 34,492 restaurants: where are they?). This first graph shows the relative number of restaurants in 2007 and 2012, with each dot representing a single country. Almost all of the 116 countries showed an increase during the five years (ie. their dots are above the pink line). The only country with a major decrease in McDonald's restaurants was Greece (to the right of the pink line), due, no doubt, to its ongoing financial problems. The country with the largest number of restaurants is, of course, the USA, with Japan a clear second.
There is also a perception that fast-food restaurants compete for customers against other types of restaurants, so that suburbs can have one or the other but not both. This can be checked using the data in the Food Environment Atlas 2014 (produced by the USDA Economic Research Service), which show the number of both Fast-food and Full-service restaurants / 1,000 popele in 2012 for each of the more than 3,100 counties in the USA. This is illustrated in the next graph, where each dot represents a single county.
For most counties, full-service restaurants actually out-number fast-food restaurants, per capita. There are even a few counties that have no fast-food places at all, but also a few with no full-service restaurants. There are even a few with neither restaurant type, notably in AK (2 counties), KY and ND. Interestingly, 3 out of the 4 counties with the largest density of full-service restaurants are in CO (including one not shown because it is off the top of the graph).
Nevertheless, you can't go far in the USA without encountering a fast-food place. As shown in a previous post (Fast-food maps), Subway has the largest number of establishments, not McDonald's. The Flowing Data blog has recently compiled a couple of maps showing the dominance of Subway in the sandwich business (Where Subway dominates its sandwich place competition, basically everywhere). This map shows the subway dominance — each dot is an area with a 10-mile radius, colored by the brand of the nearest sandwich chain.
Unfortunately, studying the effects of geography on access to fast food is not as simple as it might seem. Large-scale patterns such as those shown above are only part of the picture, because access to fast food is usually assumed to be determined at a very local scale — how far from you is the nearest fast-food place, and how easy is it to get there?
There have been many studies over the years, based on different methods and with different study criteria. These have been summarized (from different perspectives) by SE Fleischhacker, KR Evenson, DA Rodriguez, AS Ammerman (2010. A systematic review of fast food access studies. Obesity Reviews 12: e460) and LK Fraser, KL Edwards, J Cade, GP Clarke (2010. The geography of fast food outlets: a review. International Journal of Environmental Research and Public Health 7: 2290-2308).
Their conclusions from their worldwide literature reviews include:
- most studies indicated fast-food restaurants were more prevalent in low-income areas compared with middle- to higher-income areas (ie. there is a positive association between availability of fast-food outlets and increasing socio-economic deprivation);
- most studies found that fast food restaurants were more prevalent in areas with higher concentrations of ethnic minority groups;
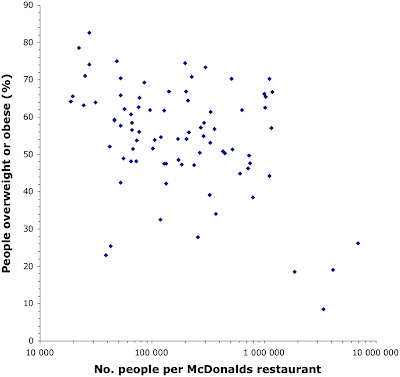
- those studies that included overweight or obesity data (usually measured as the body mass index) showed conflicting results between obesity / overweight and fast-food outlet availability — most studies found that higher body mass index was associated with living in areas with increased exposure to fast food, but the remaining studies did not find any such association;
- there is some evidence that fast food availability is associated with lower fruit and vegetable intake.
These patterns have continued over the five years since the reviews appeared, with published studies both pro (eg. J Currie, S DellaVigna, E Moretti, V Pathania. 2010. The effect of fast food restaurants on obesity and weight gain. American Economic Journal: Economic Policy 2: 32-63) and con (AS Richardson, J Boone-Heinonen, BM Popkin, P Gordon-Larsen. 2011. Neighborhood fast food restaurants and fast food consumption: a national study. BMC Public Health 11: 543) the association between fast food availability and health. To them has been added the issue of Type II diabetes and fast-food consumption (see DH Bodicoat et al. 2014. Is the number of fast-food outlets in the neighbourhood related to screen-detected type 2 diabetes mellitus and associated risk factors? Public Health Nutrition 18 : 1698-1705).
Moving on, people have also considered how the role of restaurants might define the identity of American cities. For example, Zachary Paul Neal has considered whether US cities can be classified on the basis of the local prevalence of specific types of restaurants (2006. Culinary deserts, gastronomic oases: a classification of US cities. Urban Studies 43: 1-21). He counted the numbers of several different types of restaurants in 243 of the most populous cities in the USA, and ended up classifying them into four distinct city types: Urbane oases (where one finds an abundance of restaurants of all sorts), McCulture oases (which have larger than normal concentrations of "highly standardised eating places designed for mass consumption"), Urbane deserts and McCulture deserts (both of which have fewer restaurants than their respective oasis counterpart).
Unfortunately, this sort of classification approach is self-fulfilling, because any mathematical grouping algorithm will form groups, by definition, even if there are no groups in the data. I have shown this a number of times in this blog (eg. Network analysis of scotch whiskies; Single-malt scotch whiskies — a network). These culinary data are thus crying out for a network analysis, and I would normally present one at this point in the blog post. However, I do not have a copy of Neal's dataset.
So, instead, I will finish by analyzing some data on the salt content of fast food (E Dunford et al. 2012. The variability of reported salt levels in fast foods across six countries: opportunities for salt reduction. Canadian Medical Association Journal 184: 1023-1028).
The authors collected data on the salt content of products served by six fast food chains that operate in Australia, Canada, France, New Zealand, the United Kingdom and the United States — Burger King, Domino’s Pizza, Kentucky Fried Chicken, McDonald’s, Pizza Hut and Subway. The product categories included: savoury breakfast items, burgers, chicken products, french fries, pizza, salads, and sandwiches. Data were collated for all of the products provided by all of the companies that fitted into these categories (137-523 products per country). Mean salt contents and their ranges were calculated, and compared within and between countries and companies.
We can use a phylogenetic network to visualize these data. As usual, I have used the manhattan distance and a neighbor-net network. The result is shown in the next figure. Countries that are closely connected in the network are similar to each other based on their fast-food salt content, and those that are further apart are progressively more different from each other.
You will note that the North American countries are on one side of the network, with the highest salt content, while the European countries are on the other, with the lowest salt content (on average 85% of the American salt content). This difference was reflected even between the same products in different countries — for example, McDonald's Chicken McNuggets contained 0.6 g of salt per 100 g in the UK but 1.6 g of salt per 100 g in the USA). As the authors note: "the marked differences in salt content of very similar products suggest that technical reasons are not a primary explanation."