Monday, August 31, 2015
The solution to the spinach fallacy?
Last week I blogged about Spinach and the iron fallacy. I analysed an early set of data by Thomas Richardson (1848), who calculated the amount of iron in combusted ash for various vegetables and fruits, and showed that spinach is not at all unusual in its constituents. The idea that spinach is rich in iron is untrue, and the story about a mis-placed decimal point seems to be nothing more than an urban myth.
In the meantime, Joachim Dagg, at the Natural History Apostilles blog, has reanalysed Richardson's data and revealed that The first source for the spinach-iron myth is likely to have been a somewhat inappropriate attempt to combine his data for the percent iron values in relation to the ash with the percent values of the ashes in relation to the fresh matter.
So, I have recalculated the phylogenetic network using these "adjusted" values. I used the percent values of the chemical constituents in relation to the pure ash (raw ash minus carbonic acid, charcoal and sand), and combined them with the percent values of the ashes. The issue here is that radish roots and leaves have the largest ash values, followed by cherry stems and spinach. This leads to an over-statement of the chemical contents. In particular, the iron content moves spinach from being ranked sixth to second (behind radish foliage, which is not usually eaten).
Wednesday, August 26, 2015
Request for datasets
During one of the discussion sessions at the recent Phylogenetic Network Workshop, in Singapore, the need was re-iterated for "gold standard" empirical datasets, in order to aid the development and validation of algorithms for phylogenetic networks.
The current collection of such datasets is located on this blog, at:
http://phylonetworks.blogspot.se/p/datasets.htmlHowever, it is still quite a small database, as so far it has been based solely on my own ability to locate suitable datasets that are freely available (see the comments in Public availability of phylogenetic data).
I would therefore like to remind everyone that if you have, or know of, suitable empirical datasets then please contact me.
The database is currently hierarchically arranged as follows:
Datasets where the history is a tree
Datasets where the history is known from experimentation
Datasets where the history is known from retrospective observation
Datasets where the history is reticulated
Datasets where the history is known from experimentation
Hybridization
Contamination
Datasets where the reticulation is inferred
Hybridization
Recombination
Lateral Gene Transfer
The basic requirement for a "gold standard" dataset that contains one or more reticulations (ie. there is gene flow) is that the evidence for the reticulation(s) is independent of the particular dataset. That is, there should be either experimental data, or at least another independent dataset, confirming the gene flow. This is quite a tough criterion, particularly for lateral gene transfer, but it is a necessary quality criterion.
Finally, the database requires the processed data (eg. a multiple sequence alignment), rather than the original raw data (see the comments in Releasing phylogenetic data).
Monday, August 24, 2015
Spinach and the iron fallacy
A few weeks ago, the Natural History Apostilles blog ran a series of posts on the origins of the well-known spinach-is-rich-in-iron fallacy. This is more complex than expected. Spinach was originally alleged to have been incorrectly claimed to be rich in iron due to a mis-placed decimal point in a set of comparative data. In fact, this explanation itself seems to be untrue (read the posts).
In the blog posts, Joachim Dagg traced the origins of the alleged explanation, in detail, looking at (almost) all of the relevant historical data. One of the earliest sources of data on spinach turns out to be itself something of a mystery:
Thomas Richardson (1848) Beiträge zur chemischen Kenntnis der Vegetabilien. Annalen der Chemie und Pharmacie LXVII Bd. 3.This was a single-page fold-out table (without page number) included at the end of volume 67 of the journal. In modern electronic copies, it has been erroneously attached to the last article in that issue.
The table contains values for a range of compounds in the ash produced from a variety of plants and their parts. These data are ripe for a visualization.
As usual, we can use a phylogenetic network as a form of exploratory data analysis, to compare all of the plants in a single diagram. I first normalized the data (since the compounds have very different ranges), and then used the manhattan distance to calculate the similarity of the plants based on their constituents. This was followed by a Neighbor-net analysis to display the between-plant similarities as a phylogenetic network. So, plants (or their parts) that are closely connected in the network are similar to each other based on their chemistry, and those that are further apart are progressively more different from each other.
As you can see, spinach is not particularly unusual in its chemical constituents. Indeed, it is radish, leek and asparagus that are the most unusual.
Note: there is a follow-up post indicating why spinach might have been singled out as having a high iron content: The solution to the spinach fallacy?
Wednesday, August 19, 2015
Systematic Biology
I thought that I should draw your attention to the current issue of the journal Systematic Biology, which contains more contributions about reticulate relationships than I have seen there before.
These include:
♦ Andrew R. Francis and Mike Steel (2015) Which phylogenetic networks are merely trees with additional arcs? Systematic Biology 64: 768-777. doi:10.1093/sysbio/syv037
A theoretical paper discussed by Leo in a previous blog post (Networks vs augmented trees).
♦ Jonathan Brassac and Frank R. Blattner (2015) Species-level phylogeny and polyploid relationships in Hordeum (Poaceae) inferred by next-generation sequencing and in silico cloning of multiple nuclear loci. Systematic Biology 64: 792-808. doi:10.1093/sysbio/syv035
Contains a tree of relationships among the diploid species, with the tetraploid and hexaploid species manually added as reticulations, to create a hybridization network.
♦ Noah W. M. Stenz, Bret Larget, David A. Baum, and Cécile Ané (2015) Exploring tree-like and non-tree-like patterns using genome sequences: an example using the inbreeding plant species Arabidopsis thaliana (L.) Heynh. Systematic Biology 64: 809-823. doi:10.1093/sysbio/syv039
Contains a series of trees but no network. Nevertheless, the authors' analyses "identify instances of introgression and detect one clear case of reticulation among ecotypes that have come into contact".
♦ David A. Morrison (2015) Aristotle's Ladder, Darwin's Tree: The Evolution of Visual Metaphors for Biological Order, by J. David Archibald. Systematic Biology 64: 892-895. doi:10.1093/sysbio/syv038
A book review that castigates the book's author for hardly mentioning networks when writing about phylogenetic metaphors. There is a table summarizing some of the relevant publication history.
There is also one paper that possibly should be about networks but doesn't actually mention them.
♦ Thomas C. Giarla and Jacob A. Esselstyn (2015) The challenges of resolving a rapid, recent radiation: empirical and simulated phylogenomics of Philippine shrews. Systematic Biology 64: 727-740. doi:10.1093/sysbio/syv029
The authors collected data on "hundreds of ultraconserved elements and whole mitochondrial genomes" from multiple individuals of several species of shrews (Crocidura). They conclude that "the low support we obtained for backbone relationships ... reflects a real and appropriate lack of certainty. Our results illuminate the challenges of estimating a bifurcating tree in a rapid and recent radiation, providing a rare empirical example of a nearly simultaneous series of speciation events".
A NeighborNet analysis of the provided mitochondrial data is shown in the first figure. Clearly, all it says is that the individuals group into species, but there is no information in the data about the relationships among the species.
A NeighborNet analysis of the SNPs from the ultraconserved elements is shown in the second figure. This network is not that different, in that it does little more than group the individuals into species, with little information about relationships.
However, note also that the largest reticulation involves sp_FMNH146788 and mindorus_FMNH221890. These two samples are not closely related in the mitochondrial network. This hints that the sp_FMNH146788 sample may be a genotypic mixture, due perhaps to hybridization or introgression. The authors treat the specimen as representing a "heretofore undescribed taxon that shares introgressed mitochondrial DNA with true C. ninoyi."
Labels:
Phylogeny
Monday, August 17, 2015
PhD thesis lengths
Bioinformatics lies at the nexus of the biological sciences and the computational sciences. Therefore it is sometimes worth comparing these two disciplines.
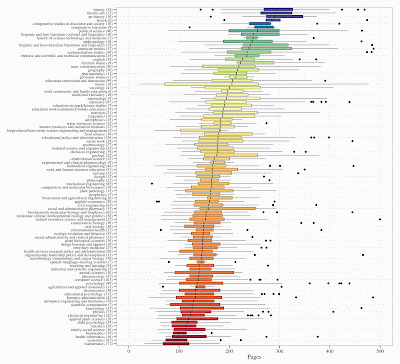
Marcus Beck at the R is My Friend blog has looked at doctoral dissertation lengths via the digital archives at the University of Minnesota. His data are shown in this box plot. You can search through it for your own favorite discipline (click on the image to make it larger).
He also has several other graphical views in his blog post, including data on masters theses.
Marcus Beck at the R is My Friend blog has looked at doctoral dissertation lengths via the digital archives at the University of Minnesota. His data are shown in this box plot. You can search through it for your own favorite discipline (click on the image to make it larger).
He also has several other graphical views in his blog post, including data on masters theses.
Labels:
Bioinformatics
Wednesday, August 12, 2015
The complexity of lexical change
Most computational approaches to historical linguistics, be it those producing networks or those producing trees, make use of lexical data. There are several reasons for this preference. Lexical data is much easier to handle than abstract grammatical data. Many linguists also think that lexical data is more representative of language evolution in general, and thus offers a much better starting point for inferences. Whether one likes the preference for lexical data or not, it seems to be worthwhile in this context to reflect a bit more about the nature of lexical data and the complexities of lexical change. This may help to get a clearer picture of the differences between language history and biological evolution.
What Makes a Word?
In a very simple language model, the lexicon of a language can be seen as a bag of words. A word, furthermore, is traditionally defined by two aspects: its form and its meaning. Thus, the French word arbre can be defined by its written form arbre or its phonetic form [ɑʁbʁə], and its meaning "tree". This is reflected in the famous sign model of Ferdinand de Saussure (Saussure 1916), which I have reproduced in [A] in the graphic below. In order to emphasize the importance of the two aspects, linguists often say that form and meaning of a word are like two sides of the same coin (see [B] in the graphic below). But we should not forget that a word is only a word if it belongs to a certain language! From the perspective of the German or the English language, for example, the sound chain [ɑʁbʁə] is just meaningless. So, instead of two major aspects of a word, we may better talk of three major aspects: form, meaning, and language. As a result, our bilateral sign model becomes a trilateral one, as I have tried to illustrate in [C] in the graphic below.What is Lexical Change?
If there was no lexical change, the lexicon of languages would remain stable during all times. Words might change their forms by means of regular sound change, but there would always be an unbroken tradition of identical patterns of denotation. Since this is not the case, the lexicon of all languages is constantly changing. Words are lost, when the speakers cease to use them, or new words enter the lexicon when new concepts arise, be it that they are borrowed from other languages, or created from native material via different morphological processes. Such processes of word loss and word gain are quite frequent and can sometimes even be observed directly by the speakers of a language when they compare their own speech with the speech of an elder or a younger generation.An even more important process of lexical change, especially in quantitative historical linguistics, is the process of lexical replacement. Lexical replacement refers to the process by which a given word A which is commonly used to express a certain meaning x ceases to express this meaning, while at the same time another word B, which was formerly used to express a meaning y, is now used to express the meaning x. The notion of lexical replacement is thus nothing else than a shift in the perspective on semantic change (as one major dimension of lexical change, see below). While semantic change is usually described from a semasiological perspective, i.e. from the perspective of the form, lexical replacement describes semantic change from an onomasiological perspective, i.e. from the perspective of the meaning.
Three Dimensions of Lexical Change
Gévaudan (2007) distinguishes three dimensions of lexical change: the morphological dimension, the semantic dimension, and the stratic dimension. The morphological dimension points to changes in the outer form of the words which are not due to regular sound change. As an example of this type of change, consider English birth and its ancestral form Proto-Germanic*ga-burdi "birth" — while the meaning of the word did not change (or at
least only slightly), the English word apparently lost the prefix ga-. This prefix
is still present in the German Geburt "birth", but it was lost without
leaving a trace in English.The loss of prefixes is not the only way in which words can change during language evolution. We also find that prefixes or suffixes are added, as, for example, in French soleil "sun", which goes back to Latin soliculus "small sun, sunny" which is itself a derivation of Latin sol "sun". The semantic dimension is illustrated by changes like the one from Proto-Germanic
*sælig "happy" to English silly.The stratic dimension refers to changes involving the exchange of words between languages, that is, processes of borrowing, in which a word is transferred from one stratum of a language to another. An example for this type of change is English mountain which was borrowed from Old French montaigne "mountain".
Note that these three dimensions of lexical change correspond directly to the three major aspects constituting a linguistic sign (or a word) that I mentioned above: The morphological dimension changes the form of a word, the semantic dimension changes its meaning, and the stratic dimension its language. Thus, the three dimensions of lexical change, as proposed by Gévaudan (2007), find their direct reflection in the major dimensions according to which words can vary.
During language evolution, lexical change processes interact in all three dimensions, and yield complex patterns which may be very hard to uncover for historical linguists. As an example of this complexity, consider the development of Proto-Indo-European
*bʰreu̯Hg̑-* "to use", as depicted in the
graphic below, which was originally designed by Hans Geisler (Heinrich-Heine
University, Düsseldorf), who kindly allowed me to reproduce it here. In the
graphic, changes in the stratic dimension are illustrated with the help of dotted
arcs (the legend labels this as "borrowed from"), and changes in the
morphological dimension are indicated by double arcs (labelled as "derived
from"). The semantic dimension is not specifically labelled as such, but one
can easily detect it by comparing the meanings of the words.Modeling Lexical Change
If we look at different historical relations from the perspective of the three dimensions of lexical change, it becomes obvious that the terminology we use in linguistics is rather fuzzy. I mentioned this in an earlier post, where I pointed to the different shades of cognacy, which were never really settled in a satisfying way in historical linguistics. If we look at this again from the perspective of the three dimensions, it is much easier to become clear about the origin of these different historical relations between words.If we investigate the different uses of the term "cognacy", for example, it becomes obvious that the differences result from controling for one or more of the three dimensions of lexical change. The traditional Indo-Europeanist notion of cognacy, for example, controls the stratic dimension by requiring stratic continuity (no borrowing), but at the same time it is indifferent regarding the other two dimensions. Cognacy à la Swadesh (especially Swadesh 1955), as we know it from the popular computational approaches which model lexical change as a process of cognate loss and gain, is indifferent regarding morphological continuity, but controls the semantic and the stratic dimensions by only considering words that have the same meaning and have not been borrowed (at least in theory).
In the table below, I have attempted to illustrate in which way the different terms, including the biological terms of homology, orthology, paralogy, and xenology, cover processes by controling each for one or more of the three dimensions of lexical change (with "+" indicating that continuity is required, "-" indicating that change is required, and "+/-" indicating indifference.) Contrasting the different dimensions of lexical change with the terminology used to refer to different relations between words shows not only the arbitrariness of the traditional linguistic terminology (why do we only cover two out of 3 * 3 * 3 = 27 different possible types? why do we only control by requiring continuity, not change? etc.), but also the fundamental difference between biological and linguistic terminology.
Concluding Remarks
So far, all computational methods that have been proposed for historical linguistics are based on the strict Swadesh type of wordlist encoding, which in the end controls for the semantic and stratic dimensions of lexical change and is indifferent regarding morphology. Such an encoding is per se inconsistent, since there is no reason to assume that morphological change would be less frequent or less indicative of language history than any of the other types.The reason why linguists tend to control for meaning when creating their datasets is mostly due to problems of sampling: it is much easier to draw a set of words from a couple of languages by starting from a given set of meanings. However, it may be useful to relax this criterion, since the restricted sets of only about 200 meanings on average necessarily hide vivid and interesting processes of lexical change.
The reasons why linguists control for borrowing are only historical, and in many cases also not feasible, since our evidence for borrowing may be limited, especially in cases where the majority of speakers is bilingual (which is more often the rule than the exception in the languages of the world). It seems much more fruitful to revive our network thinking in linguistics and to invest into the development of high quality datasets with a less arbitrary exclusion of certain dimensions of lexical change, and transparent computational methods which do not exclusively stick to the tree model.
References
- Gévaudan, P. (2007) Typologie des lexikalischen Wandels [Typology of lexical change]. Tübingen: Stauffenburg.
- Swadesh, M. (1955) Towards greater accuracy in lexicostatistic dating. International Journal of American Linguistics. Vol. 21(2), pp. 121- 137.
- Saussure, F. de (1916) Cours de linguistique générale [Course on general linguistics]. Lausanne: Payot.
Monday, August 10, 2015
The decline of marriages in the USA
The United States government likes to keep an eye on its populace, as we all know, and they keep track of numbers, as well as people. Sometimes, they release these numbers, so that we can have a look at them.
The National Center for Health Statistics, which is part of the Centers for Disease Control and Prevention, is an organization that regularly releases its data, particularly those compiled in the National Vital Statistics System. One such dataset that might be of interest is that on Marriages and Divorces.
This dataset has two tables (one for marriages and one for divorces), each provided with a convenient breakdown by state. It covers the years 1990, 1995, and 1999-2011 inclusive; and the data are rates, expressed as "per 1,000 total population residing in area."
If we simply average the data for the whole country, the graph looks like the following. Basically, the divorce rate has remained approximately constant, while the marriage rate has decreased during the current century. The actual number of marriages per year, across the country, decreased from 3.1 million in 1990 to 2.1 million in 2009-2011.
We can now look at whether the marriage trend is consistent across all of the states. As usual, we can use a phylogenetic network as a form of exploratory data analysis, to compare all of the states in a single diagram. I first used the gower similarity to calculate the similarity of the states based on the marriage rates for all of the years. This was followed by a Neighbor-net analysis to display the between-state similarities as a phylogenetic network. So, states that are closely connected in the network are similar to each other based on their marriage rates, and those that are further apart are progressively more different from each other.
The states are neatly arranged in the network in decreasing order of marriage rate from top to bottom-left. I have labeled only the those states with the highest rates.
The result for Nevada surprises no-one who has seen the honeymoon behavior of Americans — the high rate refers to those visitors getting married in Las Vegas, the self-proclaimed "Entertainment Capital of the World". The claim itself may be doubtful (Paris, for example, gets more tourists per year), but the large number of non-residents getting married in Las Vegas is not in doubt. Similarly, Hawaii is a well-known holiday destination for honeymooners, some of whom don't get married until they get there; so this rate does not reflect the behavior of the locals alone.
However, for the other labeled states the rate does seem to reflect the behavior of the residents. It is an interesting mix of states from around the country, although several of the states are from the South, while others have a large Mormon population.
Finally, we can look at whether the decline in marriage rate is repeated across the states. I have plotted the data only for the five states with the highest rates. Note that the vertical axis is on a logarithmic scale.
You will note the steep reduction in the number of people traveling to Nevada to get married, but not so for Hawaii, which has actually increased somewhat. The other states reflect the fact that there has been a general decline in marriage rate throughout the USA since the turn of the century.
Labels:
Anthropology,
EDA
Wednesday, August 5, 2015
First millennium problem has been solved: tree containment is easy on stable networks
One of the most fundamental computational problems related to phylogenetic networks is the following Tree Containment problem. Given a phylogenetic network and a phylogenetic tree, does the network display the tree? (Basically meaning that the tree can be obtained from the network by deleting nodes and branches.)
This problem was shown to be NP-hard in this paper in 2008. So, not only is it difficult to reconstruct phylogenetic networks, it is even difficult to check if a given network is consistent with certain gene trees or the estimated species tree.
In this paper in 2010, Charles Semple, Mike Steel and I studied for which classes of networks this problem remains hard and for which ones it becomes easy. In particular, we showed that the problem becomes polynomial-time solvable on so-called binary tree-child networks.
However, we were not able to extend our algorithm to a more general class of networks called reticulation visible networks, which were later called stable networks by others. A network is reticulation visible if, for each reticulation r, there exists a leaf x such that, if one would delete r, there would be no more directed path from the root to x. The idea behind this class of networks is that the leaf x gives us some information about the reticulation r. And how can we possibly expect to reconstruct reticulations if we don't have any information about them? Moreover, the class of reticulation visible networks seems to be much larger than the class of tree-child networks.
We advertised this open problem as Problem 4 in a list of seven important open computational problems related to phylogenetic networks in this blog post. Recently, there has been quite some interest in the problem, and two papers have presented algorithms for restricted subclasses. A solution for the whole class of binary stable networks has now been proposed in:
Andreas D.M. Gunawan, Bhaskar DasGupta, Louxin Zhang. Stability Implies Computational Tractability: Locating a Tree in a Stable Network is Easy. arXiv:1507.02119 [q-bio.PE]
The paper has not been published yet, but the proof seems correct to me, and is very clever and elegant. Hence, the first of the seven "phylogenetic network millennium problems" has been solved!
Below you see Louxin Zhang presenting the algorithm at the Phylogenetic Networks workshop in Singapore.
This problem was shown to be NP-hard in this paper in 2008. So, not only is it difficult to reconstruct phylogenetic networks, it is even difficult to check if a given network is consistent with certain gene trees or the estimated species tree.
In this paper in 2010, Charles Semple, Mike Steel and I studied for which classes of networks this problem remains hard and for which ones it becomes easy. In particular, we showed that the problem becomes polynomial-time solvable on so-called binary tree-child networks.
However, we were not able to extend our algorithm to a more general class of networks called reticulation visible networks, which were later called stable networks by others. A network is reticulation visible if, for each reticulation r, there exists a leaf x such that, if one would delete r, there would be no more directed path from the root to x. The idea behind this class of networks is that the leaf x gives us some information about the reticulation r. And how can we possibly expect to reconstruct reticulations if we don't have any information about them? Moreover, the class of reticulation visible networks seems to be much larger than the class of tree-child networks.
We advertised this open problem as Problem 4 in a list of seven important open computational problems related to phylogenetic networks in this blog post. Recently, there has been quite some interest in the problem, and two papers have presented algorithms for restricted subclasses. A solution for the whole class of binary stable networks has now been proposed in:
Andreas D.M. Gunawan, Bhaskar DasGupta, Louxin Zhang. Stability Implies Computational Tractability: Locating a Tree in a Stable Network is Easy. arXiv:1507.02119 [q-bio.PE]
The paper has not been published yet, but the proof seems correct to me, and is very clever and elegant. Hence, the first of the seven "phylogenetic network millennium problems" has been solved!
Below you see Louxin Zhang presenting the algorithm at the Phylogenetic Networks workshop in Singapore.
Monday, August 3, 2015
Networks vs augmented trees
The distinction between networks and augmented trees is interesting from a biological, computational and mathematical point of view. An augmented tree is the result of adding cross-connecting branches to a tree, turning it into a network. So each augmented tree is a network (called a tree-based network). But is each network an augmented tree? In a previous blog post we showed that this is not the case. There exist networks that are inherently network-like and cannot be obtained by adding branches to a tree. (If we are allowed to create new nodes by subdividing branches of the tree, but are not allowed to subdivide any of the previously-added branches.)
The biological question here is as follows: is evolution a tree-like process augmented with horizontal events, or is evolutionary inherently network-like?
This concept is also relevant to phylogenetic network reconstruction approaches, because several such methods work by adding edges to an estimated species tree. Therefore, there exist networks that will always be missed by such methods.
Interestingly, it has turned out that it is easy to find out if a given network is tree-based or not. A polynomial-time algorithm was presented recently by Francis and Steel:
Andrew Francis and Mike Steel, Which Phylogenetic Networks are Merely Trees with Additional Arcs? Systematic Biology (2015).
They solve the problem by reducing it to a model called 2-SAT, which is interesting because it automatically leads to a very simple and fast algorithm solving the problem.
An interesting question that remains open is the following. Given a network and a tree, can we decide in polynomial time if the network can be obtained by adding edges to the given tree? Another question is whether there exists a clean graph-theoretic characterisation of tree-based networks.
Below you see Mike Steel presenting their recent paper at the Phylogenetic Networks Workshop in Singapore. He also discussed other recent results, concerning folding and unfolding phylogenetic trees and networks, as well as distance-based methods for detecting reticulation.
The biological question here is as follows: is evolution a tree-like process augmented with horizontal events, or is evolutionary inherently network-like?
This concept is also relevant to phylogenetic network reconstruction approaches, because several such methods work by adding edges to an estimated species tree. Therefore, there exist networks that will always be missed by such methods.
Interestingly, it has turned out that it is easy to find out if a given network is tree-based or not. A polynomial-time algorithm was presented recently by Francis and Steel:
Andrew Francis and Mike Steel, Which Phylogenetic Networks are Merely Trees with Additional Arcs? Systematic Biology (2015).
They solve the problem by reducing it to a model called 2-SAT, which is interesting because it automatically leads to a very simple and fast algorithm solving the problem.
An interesting question that remains open is the following. Given a network and a tree, can we decide in polynomial time if the network can be obtained by adding edges to the given tree? Another question is whether there exists a clean graph-theoretic characterisation of tree-based networks.
Below you see Mike Steel presenting their recent paper at the Phylogenetic Networks Workshop in Singapore. He also discussed other recent results, concerning folding and unfolding phylogenetic trees and networks, as well as distance-based methods for detecting reticulation.
Subscribe to:
Posts (Atom)